Optimizing Data Simplification: Principal Component Analysis for Linear Dimensionality Reduction

 Data Matrix

Imagine a dataset containing 138 grayscale images, each with a resolution of $93 \times 70=3810$ pixels and a grayscale range extending from 0 to 255.   By converting these images into vector form, we represent the dataset as $\{\mathbf{x}^{(k)}\}_{k=1}^{138}$, with each vector $\mathbf{x}^{(k)}$ residing in a portion of $3810$-dimensional discrete Euclidean space, specifically $\{0, 1, \ldots, 255\}^{3810}$.  In the subsequent figure, $130$ is the total count of images, while $3810$ is the pixel count per image.

                          
This transformation yields a data matrix, denoted by $X$, composed of 138 columns—each row uniquely mapping to an image—and $3810$ rows, which correlate to the pixel values. This organized matrix becomes a critical tool for a variety of analytical processes, such as uncovering  common patterns within the images, the application of dimensionality reduction to enhance data manageability, implementing dimensionality reduction techniques, or developing a machine learning model for recognition purposes.  

Exploring Data Characteristics: Mean, Standard Deviation, Covariance, and the Gram Matrix

For a clearer understanding, let's examine the matrix $X$, which has dimensions $138 \times 3810$. Here, $138$ represents the total number of images, while $3810$ corresponds to the pixel count in each image. The mean vector of $X$ is defined as $$\bar{\mathbf{x}} =\frac{1}{138} \sum_{k=1}^{138}\mathbf{x}^{(k)}$$
The standard deviation of $X$, indicated by $\text{std}(X)$, measures the spread of the dataset:
$$\text{std}(X)== \sqrt{\frac{1}{138} \sum_{k=1}^{138}\|\mathbf{x}^{(k)} - \bar{\mathbf{x}}\|^2}.$$

The variance, $\sigma^2$, is simply the square of the standard deviation.
The covariance matrix of $X$, which is a $3810 \times 3810$ matrix, conveys both the variance and covariance within the data:
$$\text{cov}(X, X)= \frac{1}{137}  X^TX - \bar{\mathbf{x}}\bar{\mathbf{x}}^T,$$
where "T" denotes the transpose.

The Gram matrix of $X$, with dimensions $138 \times 138$, captures the similarities (or differences) among the data points. The element $G_{ij}$ in the Gram matrix is the inner product between the mean-adjusted vectors: $$G_X== (X - \mathbf{1}\bar{\mathbf{x}}^T)(X - \mathbf{1}\bar{\mathbf{x}}^T)^T,$$
where $\mathbf{1}$ is a vector of 138 ones. This expression underscores the Gram matrix's utility in evaluating interactions among data points in $X$. The Gram matrix also plays a pivotal role in applications like styleGAN, showcasing its versatility in advanced image analysis techniques.

Principal Component Analysis

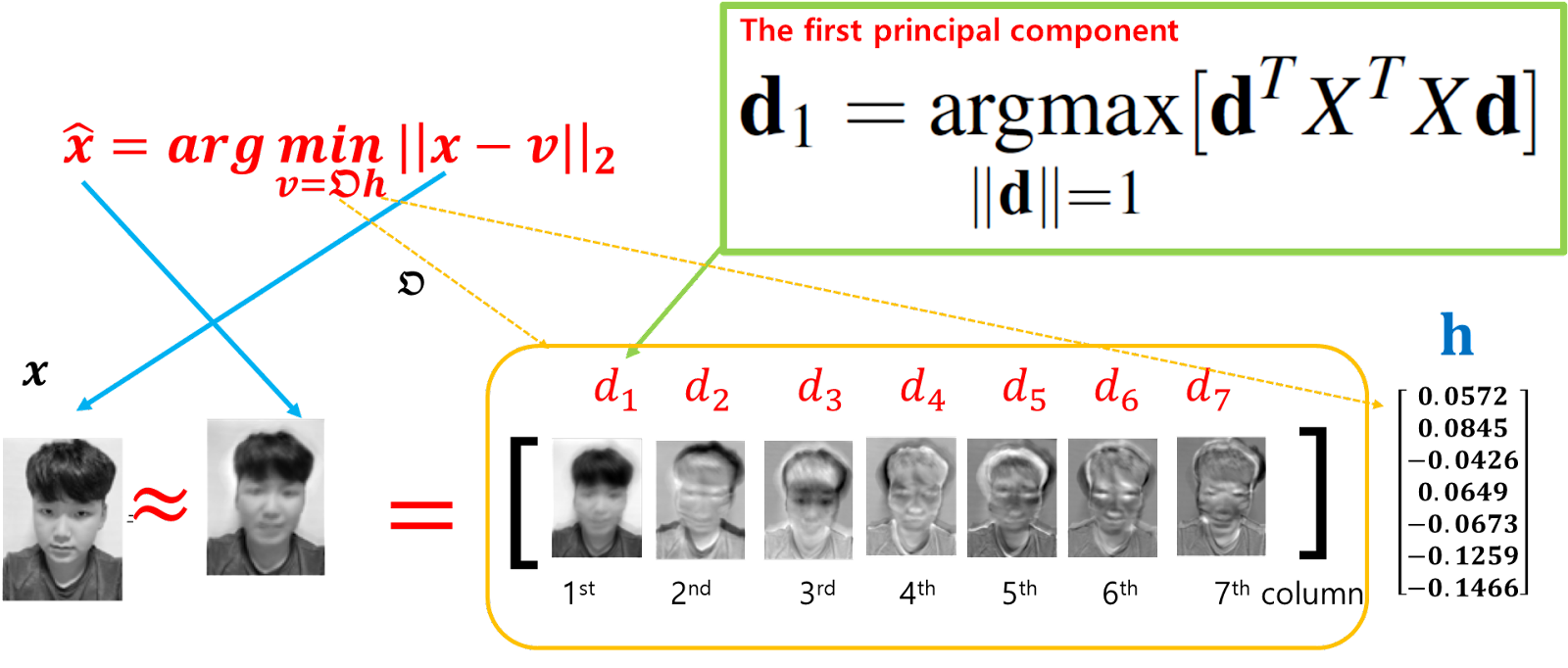
Principal Component Analysis (PCA) is a technique used to transform the data table $X$, with the goal of accentuating its similarities and differences. It is based on the assumption that the dataset, represented as $\{\mathbf{x}^{(1)}, \cdots, \mathbf{x}^{(138)}\}$, primarily exists within a linear subspace of significantly lower dimensionality than the original 3810-pixel dimension. By employing PCA, we aim to map this data onto a more manageable, 7-dimensional subspace, which is optimally aligned with the data's most significant variance directions.
 This dimensional reduction, from the original pixel dimension of 3810 to just 7, allows for a focused analysis on the core features that capture the essence of the data, despite the number of observations being only 138. The five principal components extracted in this process provide a concise, yet comprehensive, representation of the dataset.  To simplify the notation, let's assume that the data has been centered, meaning the mean of the dataset is $\bar{x} = \mathbf{0}$.  Under this assumption, the first principal component can be described as the vector $\mathbf{d}_1$ that maximizes the variance of the data in the table $X$. Formally, this is represented by the optimization problem:
$$\mathbf{d}_1=\underset{\|\mathbf{d}\|=1 }{\text{argmax}}  \left\| X-X \mathbf{d}\mathbf{d}^\top \right\|_F,$$
where $X\mathbf{d}\mathbf{d}^T$ represents the projection of $X$ onto the direction of $\mathbf{d}$ and $\| \cdot\|_F$ represents the Frobenius norm.
Here, $\mathbf{d}_1$ is the direction in the data's feature space along which the data's variance is maximized, subject to the constraint that the norm of $\mathbf{d}$ is 1. 
Similarly, to identify the second principal component, $\mathbf{d}_2$, we follow a process akin to that used for the first, but with a modification to the dataset $X$. Specifically, we adjust $X$ to account for the variance already captured by the first principal component. This adjusted dataset, $X_2$, is defined as: $$X_2= X - X\mathbf{d}_1\mathbf{d}_1^T.$$
. The second principal component, $\mathbf{d}_2$, is then determined by maximizing the variance in this adjusted dataset $X_2$, which is formally given by: $$\mathbf{d}_2 = \underset{\|\mathbf{d}\| = 1}{\text{argmax}} \left\| X_2 -X_2 \mathbf{d}\mathbf{d}^\top \right\|_F$$



This methodology effectively simplifies the data's complexity, facilitating a more efficient exploration and visualization while retaining critical structural information.

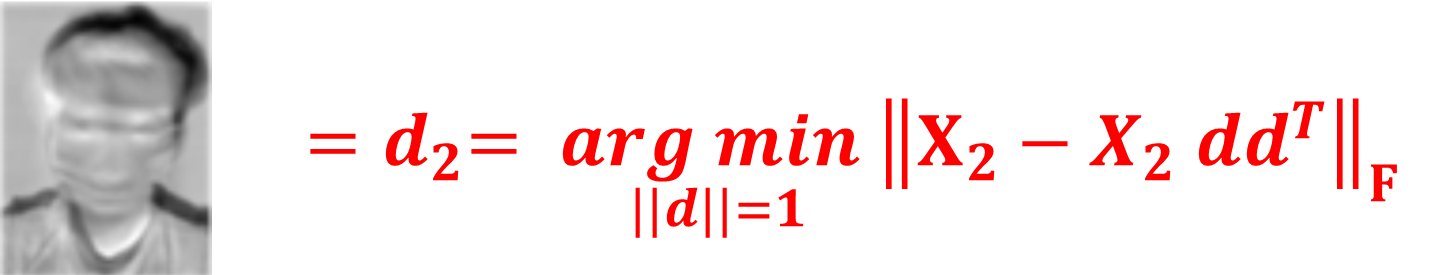
Comments

Post a Comment

Popular posts from this blog

Exploring the Fundamentals of Diffusion Models

Image
This blog post explores the recently popular diffusion models. Since there are many excellent explanations available, I don't intend to duplicate their detailed discussions. Rather, I try to offer a succinct summary that highlights the essential principles and foundational concepts behind diffusion models. Diffusion models belong to the family of generative neural network models, alongside Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs). The term "diffusion" originates from non-equilibrium thermodynamics, wherein particles (images) migrate from high concentration regions (represented by a data manifold filled with structured data) to the low concentration regions (In essence, the vast majority of points within the entire space are overwhelmingly dominated by noisy images). This concept illustrates how diffusion models iteratively refine noise into coherent, structured data by effectively reversing this natural diffusion process. To make the conc...
Read more

University Education: Reflecting Life's Complexities and Challenges

Recently, a distinct trend has been observed: students receiving considerable academic and financial backing from well-educated parents frequently gain admission to elite universities and exhibit strong academic performance during their undergraduate years.  However, a worrisome pattern has also surfaced: these students frequently struggle to achieve financial independence, relying heavily on their parents for financial assistance.  This dependence can greatly obstruct their ability to develop the crucial survival skills needed to adeptly navigate the intricacies of life in society. In this blog post, I aim to explore the question of whether a university offering comprehensive support and an optimal research environment customized for students truly benefits them in the long run. The motivation behind this discussion stems from my experience visiting a university in UAE, where I witnessed the creation of an optimal educational environment supported by significant financia...
Read more

AI as an Aid, Not a Replacement: Enhancing Medical Practice without Supplanting Doctors

In this blog, I emphasize the crucial point that AI is not a replacement for doctors. Rather, its role is to unburden doctors from the tedious tasks of keyboard input and time-consuming procedures, thereby enhancing their capabilities and allowing them to focus on what truly matters: patient care. The foremost strength of deep learning resides in its remarkable computational capacity to swiftly integrate and analyze data derived from the diagnostic decisions of numerous doctors. Essentially, deep learning models serve as rapid calculators, excelling in processing and synthesizing vast amounts of information. However, they encounter a significant limitation: unlike humans, these models struggle to adapt to new and evolving situations with the same intuition and flexibility. While recent advancements in generative models have showcased their ability to produce novel outputs, these innovations often amount to recombination of existing data. Deep learning inherently lacks the human-like ab...
Read more