Vectorization in Medical Image Analysis

Vector  

In the context of $n$-dimensional Euclidean vector space, a vector $\mathbf{x} = (x_1, x_2, \ldots, x_n)$ is characterized by its magnitude $\|{\bf x}\|=\sqrt{{\bf x}\cdot{\bf x}}=\sqrt{\sum_{k=1}^n x_k^2}$  and its direction, determined by normalizing $\mathbf{x}$ to a unit vector, $\frac{{\bf x}}{\|{\bf x}\|}$. Additionally, the angle $\theta$ between two vectors ${\bf x}$ and ${\bf x}'$  can be determined using the cosine of the angle, expressed as:$$\cos \theta=\frac{{\bf x}\cdot {\bf x}'}{ \|{\bf x} \| \|{\bf x}'\|   }.$$ 

This expression, leveraging the dot product of $\mathbf{x}$ and $\mathbf{x}'$ normalized by their magnitudes, quantifies the geometric relationship or similarity between the two vectors. It is a fundamental concept that has widespread applications in various fields, including computational geometry and machine learning.

Understanding Images as Vectors

In the specialized domain of medical imaging, modalities such as Computed Tomography (CT) and Magnetic Resonance Imaging (MRI), generate two-dimensional tomographic images. 

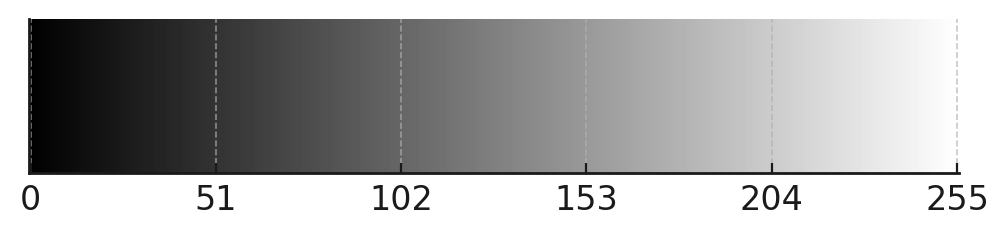
These images are composed of pixel matrices, where  each pixel, assigned a grayscale intensity value that usually spans from 0 to 255.

             

By systematically arranging each pixel's value into a sequential array, the pixel matrix of a medical image is transformed into an one-dimensional numerical vector. The figure below showcases the conversion of two-dimensional images into their vector forms.


 This transformation from a two-dimensional pixel array to a one-dimensional numerical vector facilitates various computational techniques, allowing for the application of vector-based analysis to the image. For instance, vector operations can be employed to compare images, apply transformations, or perform feature extraction, thereby extending the utility of vector concepts to the processing and analysis of medical images.

Analyzing Image Collections: Mapping to Vectors and Points in High-Dimensional Spaces

A 2D image, composed of pixels, each with 256 grayscale levels and a pixel size of $n$, can be represented as an element $\mathbf{x} = (x_1, \ldots, x_n)$ in the discrete space $\Bbb V=\{0, \ldots, 255\}^n$, where $x_k$ ($k$-th axis coordinate) corresponds to the grayscale intensity at the $k-$th pixel.

For instance, when the number of pixels is $n = 500 \times 500$, the total number of possible elements in $\Bbb V$ is astronomically large: $256^{250000}$, which far exceeds the number of atoms in the universe.
The overwhelming majority of points in $\Bbb V$ (more than $99.99999\%$) exhibit noise-like images, resembling random patterns rather than meaningful images. In contrast, points resembling actual medical images occupy a minuscule portion of the space $\Bbb V$ due to strong local and global interconnections among the pixels.


In the context of automatic or semi-automatic medical image analysis, the goal is to discover a mapping function $f: \mathbf{x} \mapsto \mathbf{y}$, wherein $\mathbf{y}$ signifies a targeted, useful outcome associated with the input medical image $\mathbf{x}$. In the domain of machine learning, the function $f$ is typically constructed as a neural network, designed to predict useful outcomes. For instance, in the image depicted below, the input $\mathbf{x}$ is a 3D Cone Beam Computed Tomography (CBCT) image, while the output represents its corresponding 3D tooth segmentation.

In supervised learning, the objective is to train a function or neural network $f$ utilizing labeled training data ${(\mathbf{x}^{(k)},\mathbf{y}^{(k)})}_{k=1}^{K}$. The learning process aims to minimize the aggregate distance between predicted outcomes and actual labels across all training examples:

$$f = \underset{f \in \mathcal{Network}}{\operatorname{argmin}} \sum_{k=1}^{K} \operatorname{dist}(f(\mathbf{x}^{(k)}), \mathbf{y}^{(k)}).$$

Here, the term $\operatorname{dist}(f(\mathbf{x}), \mathbf{y})$ measures the discrepancy between the predicted outcomes of the neural network, $f(\mathbf{x})$, and the actual outputs $\mathbf{y}$. The term "argmin" (short for "arguments of the minima") identifies a neural network configuration for which the loss function attains its lowest value. The symbol $\mathcal{Network}$ represents the set of functions enabled by a special architecture of neural networks, aimed at transforming inputs $\mathbf{x}$ into outputs $\mathbf{y}$.


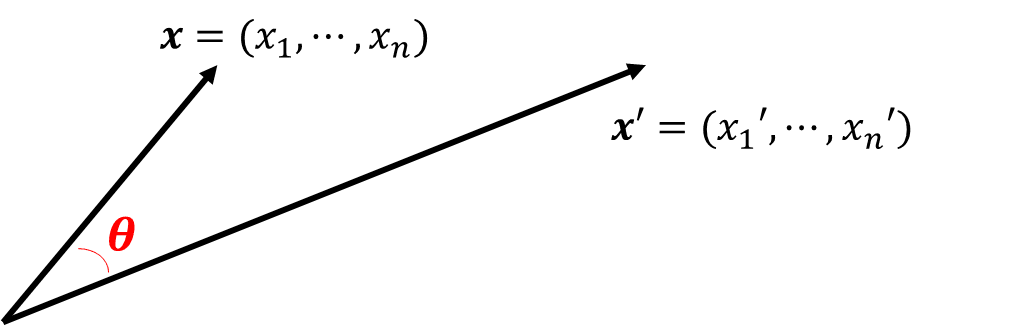
Comments

Post a Comment

Popular posts from this blog

Exploring the Fundamentals of Diffusion Models

Image
This blog post explores the recently popular diffusion models. Since there are many excellent explanations available, I don't intend to duplicate their detailed discussions. Rather, I try to offer a succinct summary that highlights the essential principles and foundational concepts behind diffusion models. Diffusion models belong to the family of generative neural network models, alongside Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs). The term "diffusion" originates from non-equilibrium thermodynamics, wherein particles (images) migrate from high concentration regions (represented by a data manifold filled with structured data) to the low concentration regions (In essence, the vast majority of points within the entire space are overwhelmingly dominated by noisy images). This concept illustrates how diffusion models iteratively refine noise into coherent, structured data by effectively reversing this natural diffusion process. To make the conc...
Read more

University Education: Reflecting Life's Complexities and Challenges

Recently, a distinct trend has been observed: students receiving considerable academic and financial backing from well-educated parents frequently gain admission to elite universities and exhibit strong academic performance during their undergraduate years.  However, a worrisome pattern has also surfaced: these students frequently struggle to achieve financial independence, relying heavily on their parents for financial assistance.  This dependence can greatly obstruct their ability to develop the crucial survival skills needed to adeptly navigate the intricacies of life in society. In this blog post, I aim to explore the question of whether a university offering comprehensive support and an optimal research environment customized for students truly benefits them in the long run. The motivation behind this discussion stems from my experience visiting a university in UAE, where I witnessed the creation of an optimal educational environment supported by significant financia...
Read more

AI as an Aid, Not a Replacement: Enhancing Medical Practice without Supplanting Doctors

In this blog, I emphasize the crucial point that AI is not a replacement for doctors. Rather, its role is to unburden doctors from the tedious tasks of keyboard input and time-consuming procedures, thereby enhancing their capabilities and allowing them to focus on what truly matters: patient care. The foremost strength of deep learning resides in its remarkable computational capacity to swiftly integrate and analyze data derived from the diagnostic decisions of numerous doctors. Essentially, deep learning models serve as rapid calculators, excelling in processing and synthesizing vast amounts of information. However, they encounter a significant limitation: unlike humans, these models struggle to adapt to new and evolving situations with the same intuition and flexibility. While recent advancements in generative models have showcased their ability to produce novel outputs, these innovations often amount to recombination of existing data. Deep learning inherently lacks the human-like ab...
Read more