Utilizing Implicit Neural Representations for Solving Ill-posed Inverse Problems

Recently, the field of medical imaging has witnessed numerous attempts aimed at producing high-resolution images with significantly insufficient measured data. These endeavors are motivated by a variety of objectives, such as reducing data acquisition times, enhancing cost efficiency, minimizing invasiveness, and elevating patient comfort, among other factors. Nevertheless, these efforts necessitate tackling severely ill-posed inverse problems, due to the significant imbalance between the number of unknown variables (needed for desired resolution) and the number of available equations (derived from measured data). 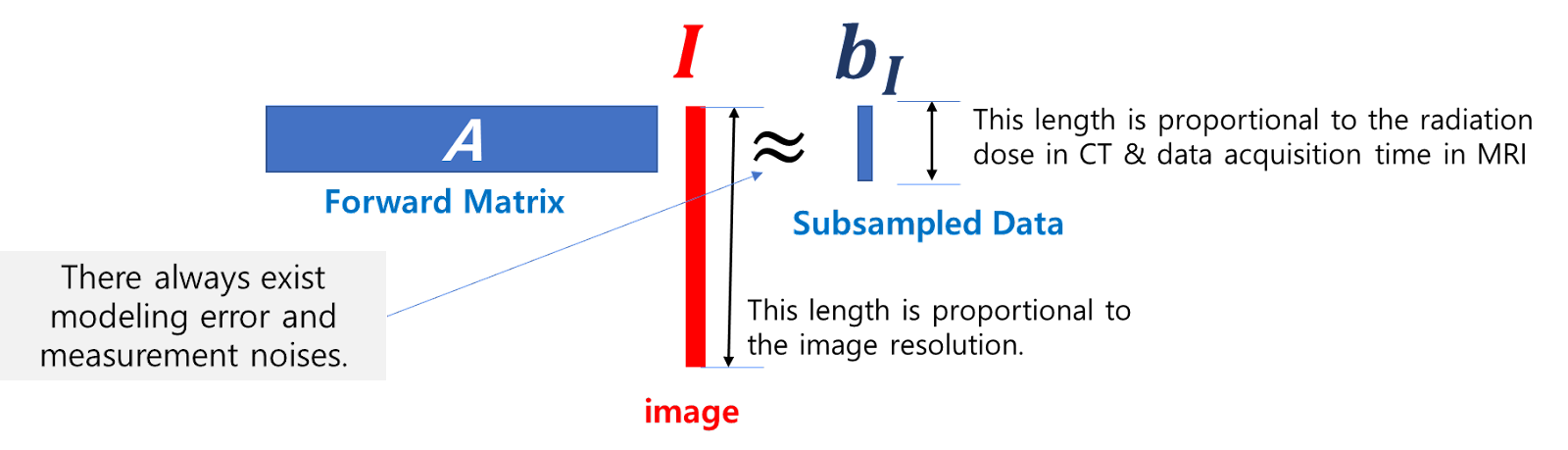For a clearer understanding, let's examine a linear system represented by $\mathbf{A}I = \mathbf{b}_{I} + \mathbf{\epsilon}$, where $\mathbf{A}$ represents an $m \times n$ matrix with a highly underdetermined scenario ($m \ll n$). This matrix $\mathbf{A}$ serves as a linearized forward model. In this formulation, $I$ is an $n$-dimensional vector representing the image to be reconstructed, $\mathbf{b}_{I}$ is the measured data correlated with $I$, having a vector size of $m$, and $\mathbf{\epsilon}$ signifies the deviation due to modeling inaccuracies and noise.

This condition of $m \ll n$ results in a severely ill-posed problem, stemming from the pronounced imbalance between the fewer equations ($m$) and the greater number of unknowns ($n$). This imbalance renders it impractical to derive an analytical expression for $I(\mathbf{x})$ at each position $\mathbf{x}$ solely based on the data $\mathbf{b}_{I}$.  Furthermore, in these severely ill-posed scenarios, traditional reconstruction approaches (represented by $I=\underset{I}{\mathrm{argmin}} | \mathbf{A}I - \mathbf{b}_{I}| +\lambda \mathrm{Reg}(I)$, where $\mathrm{Reg}(I)$ denotes regularization methods like Tikhonov, total variation minimization, or sparsity-promoting techniques) may not adequately address the complexities involved. 

To effectively tackle highly ill-posed problems, incorporating prior knowledge that comprehensively integrates both local and global interactions among grid elements into the problem-solving process is advantageous. Utilizing implicit neural representations (INRs) emerges as a promising strategy for these challenges, given that their representational efficacy is anchored in the flexibility of Multilayer Perceptrons (MLPs) rather than grid resolution. Coupling this approach with carefully selected loss functions can enable MLPs to excel in discerning the core structure of images and reducing unnecessary redundancy in their representation.

To illustrate the application of INRs simply, imagine $I$ as a head tomographic image. This image, $I$, is represented through an MLP-based function that maps every spatial coordinate $x$ to its corresponding grayscale intensity. The optimization of this mapping's parameters is achieved through a loss function that accounts for the equation $\mathbf{A}I = \mathbf{b}_{I} + \mathbf{\epsilon}$.

INRs may have a potential to offer a compelling approach to nonlinear and structured image depiction, utilizing neural networks parameterized by $\theta$ that are refined through minimizing the difference between predicted outputs and actual data. Unlike conventional methods that seek to find $I(\mathbf{x})$ at every spatial coordinate $\mathbf{x}$ (an endeavor hampered by an overwhelming number of grid elements compared to available measurements), INRs strive to reconstruct the full image $I$, which is somewhat structured with interrelated pixels, by fine-tuning $\theta$. This strategy holds the promise of capturing the comprehensive structure of $I$ by leveraging the overarching patterns and relationships among pixel positions.

Another potential benefit of INRs over conventional approaches such as $I=\underset{I}{\mathrm{argmin}} \| \mathbf{A}I - \mathbf{b}_{I}\| +\lambda \mathrm{Reg}(I)$ is their ability to avoid dependency on potentially highly corrupted image information described by $(\mathbf{A}\mathbf{A}^*)^{-1}\mathbf{A}^*\mathbf{b}_{I}$. This is particularly crucial in situations involving a highly ill-conditioned matrix $\mathbf{A}$, which may also involve  mismatches in the forward model equation $\mathbf{A}I = \mathbf{b}_{I}$ during the linear approximation process. Under these circumstances, the operation $\mathbf{A}^*\mathbf{b}_{I}$ could inadvertently introduce unwanted distortions into the authentic data $\mathbf{b}_{I}$.

In the past four years, Neural Radiance Fields (NeRF) have revolutionized computer graphics and vision by enabling the generation of highly detailed 3D models from a collection of 2D images. By leveraging an INR with a MLP neural network, NeRF maps spatial coordinates and viewing angles to color and density, allowing for the photorealistic visualization of complex scenes from new perspectives. Highlighting its influence, NVIDIA's Instant NeRF, capable of transforming 2D images into 3D scenes, earned recognition from TIME Magazine as one of the Best Inventions of 2022.

Given the wealth of high-quality video lectures on INRs and NeRFs, this blog only explained the core philosophy behind INRs.

References

[1] B. Mildenhall, P. Srinivasan, M. Tancik, J. T. Barron, R. Ramamoorthi, and R. Ng, "NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis," in Communications of the ACM, vol. 65, no. 1, pp. 99-106, 2021.

[2] T. Müller, A. Evans, C. Schied, and A. Lefohn, "Instant Neural Graphics Primitives with a Multiresolution Hash Encoding," in ACM Transactions on Graphics (TOG), vol. 41, no. 4, Article 134, 2022.

[3] J. T. Barron, B. Mildenhall, M. Tancik, P. Hedman, R. Martin-Brualla, and P. Srinivasan, "Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields," in Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021.

[4] R. Martin-Brualla, N. Radwan, M. S. M. Sajjadi, J. T. Barron, A. Dosovitskiy, and D. Duckworth, "NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections," in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021.