Practical Vector Calculus for the AI Era
This blog presents undergraduate-level vector calculus with examples and perspectives drawn from artificial intelligence. It was created in response to the limitations of many existing calculus textbooks in addressing the conceptual demands of this rapidly evolving field.
Before we begin, it is important to clarify how the variable \(\mathbf{x}\) will be used throughout the text. In classical calculus, the variable \(\mathbf{x}\) typically denotes a physical coordinate, such as position in space. In deep learning, however, \(\mathbf{x}\) often represents a token or a feature vector that encodes complex structures, including language, images, or speech. This shift reflects a transition from modeling physical space to modeling abstract, high-dimensional data spaces.
1. Vectors
Vectors are mathematical entities characterized by both magnitude and direction. They are essential for describing physical quantities such as blood flow velocity, forces acting on joints, and features in image analysis for deep learning.
- A vector in three-dimensional space is written as: \[ \mathbf{v} = v_x \hat{i} + v_y \hat{j} + v_z \hat{k}, \] where \(\hat{i} = (1,0,0)\), \(\hat{j} = (0,1,0)\), and \(\hat{k} = (0,0,1)\) are the unit vectors along the \(x\)-, \(y\)-, and \(z\)-axes, respectively. The components \(v_x\), \(v_y\), and \(v_z\) represent the magnitude of the vector in the \(x\)-, \(y\)-, and \(z\)-directions. Vectors can describe the speed and direction of blood flow in vessels, facilitating the analysis of hemodynamics. They are also used to model forces acting on prosthetic joints or tissues, aiding in the study of biomechanics and prosthetic design.
- A vector in \(n\)-dimensional space is written as: \[ \mathbf{x} = (x_1, x_2, x_3, \ldots, x_n), \] where each component \(x_j\) represents the magnitude of the vector in the \(j\)-th dimension. When the vector \(\mathbf{x}\) represents a vectorized version of an image, \(x_j\) corresponds to the grayscale intensity of the image at the \(j\)-th pixel position. This representation is commonly used in deep learning for image processing tasks.
The \(L^2\)-norm (also called the Euclidean norm) of a vector \(\mathbf{x} = [x_1, x_2, \ldots, x_n] \in \mathbb{R}^n\) is defined as: \[ \|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} = \sqrt{\sum_{i=1}^n x_i^2}. \]
- The Euclidean norm is derived from the Pythagorean theorem: for a right triangle with legs \(a\) and \(b\), and hypotenuse \(c\), it holds that: \[ c^2 = a^2 + b^2. \]
- In two dimensions (\(\mathbb{R}^2\)), the \(L^2\)-norm of a vector \(\mathbf{x} = [x_1, x_2]\) represents the length (or magnitude) of the vector. This is equivalent to the hypotenuse of a right triangle with sides \(x_1\) and \(x_2\): \[ \|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2}. \]
The distance between two vectors \(\mathbf{u} = (u_1, u_2, \ldots, u_n)\) and \(\mathbf{v} = (v_1, v_2, \ldots, v_n)\) in \(n\)-dimensional space is given by the Euclidean distance: \[ d(\mathbf{u}, \mathbf{v}) = \sqrt{\sum_{j=1}^n (u_j - v_j)^2}. \] Alternatively, in terms of the \(L^2\)-norm, the distance can be written as: \[ d(\mathbf{u}, \mathbf{v}) = \|\mathbf{u} - \mathbf{v}\|_2. \]
- The figure below illustrates that the direct Euclidean distance between the images of two different digits, such as 4 and 9, can sometimes be smaller than the distance between an image of a digit (e.g., 9) and its transformed version (e.g., a translated or rotated version of 9). This highlights the limitation of using direct Euclidean distance for digit classification in the MNIST dataset. In deep learning, instead of comparing raw pixel values, features are extracted from MNIST digit images, typically represented as embeddings or feature vectors (sometimes conceptualized as "barcodes"). These feature vectors capture the semantic structure of the images, and distances between these vectors are then used for robust digit identification.

- Face recognition is a challenging problem, primarily due to the difficulty in finding robust feature vectors that accurately represent face images. The complexity arises from various factors, such as changes in appearance over time, weight fluctuations, lighting conditions, facial expressions, and other variations. While technologies like the iPhone have achieved notable success in face recognition, they are not as reliable as fingerprint or iris recognition for high-security applications, which is why face recognition is not widely adopted for critical tasks such as airport security. In the example shown in the figure below, the two images are of the same person, and from a human perspective, the distance between them should be zero. However, deep learning-based encoding methods still face challenges in producing identical feature vectors for such cases. This highlights the need for more advanced techniques to improve the robustness and accuracy of face recognition systems.
The inner product (or dot product) measures the projection of one vector onto another.
- For three dimensions: \[ \mathbf{u} \cdot \mathbf{v}:= \langle \mathbf{u}, \mathbf{v} \rangle = u_x v_x + u_y v_y + u_z v_z, \] or equivalently: \[ \langle \mathbf{u}, \mathbf{v} \rangle = \|\mathbf{u}\|_2 \|\mathbf{v}\|_2 \cos\theta, \] where \(\theta\) is the angle between \(\mathbf{u}\) and \(\mathbf{v}\). Here, \(\langle \cdot, \cdot \rangle\) represents the inner product.
- The work done by a force \(\mathbf{F}\) moving an object along a displacement \(\mathbf{d}\) is given by: \[ W = \mathbf{F} \cdot \mathbf{d} = \|\mathbf{F}\|_2 \|\mathbf{d}\|_2 \cos\theta. \] This can be applied to calculate, for example, the energy required to push blood through a stenosed artery.
- For \(n\) dimensions: \[ \mathbf{x} \cdot \mathbf{x'} = \langle \mathbf{x}, \mathbf{x'} \rangle= \sum_{j=1}^n x_j x_j' \] where \(\mathbf{x}\) and \(\mathbf{x'}\) are \(n\)-dimensional vectors.
- When \(\mathbf{u}\) and \(\mathbf{v}\) represent two vectors, the dot product \(\mathbf{u} \cdot \mathbf{v}\) is a measure of their similarity. A larger value of \(\mathbf{u} \cdot \mathbf{v}\) indicates a greater degree of similarity between the two vectors. If the vectors \(\mathbf{u}\) and \(\mathbf{v}\) are normalized, the dot product simplifies to the cosine of the angle \(\theta\) between them: \[ \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\|\mathbf{u}\| \| \mathbf{v}\|} = \cos \theta, \] where \(\theta\) is the angle between \(\mathbf{u}\) and \(\mathbf{v}\). In this case, a larger dot product corresponds to a smaller angle, which indicates a higher level of alignment or similarity. This concept has practical applications in physics and engineering.
- For example, in feature space, we can represent the characteristics of a cat and a tiger as vectors \(\mathbf{u}_{\text{cat}} = [u_1, u_2, \ldots, u_n]\) and \(\mathbf{v}_{\text{tiger}} = [v_1, v_2, \ldots, v_n]\), where each component corresponds to a specific feature such as size, color, or texture. Once \(\mathbf{u}_{\text{cat}}\) and \(\mathbf{v}_{\text{tiger}}\) are constructed, their dot product is calculated as: \[ \mathbf{u}_{\text{cat}} \cdot \mathbf{v}_{\text{tiger}} = \sum_{i=1}^n u_i v_i = \|\mathbf{u}_{\text{cat}}\| \|\mathbf{v}_{\text{tiger}}\| \cos \theta, \] where \(\theta\) is the angle between the two vectors. If the vectors are aligned (\(\theta\) close to 0), the dot product is large, indicating high similarity. If the vectors are orthogonal (\(\theta = 90^\circ\)), the dot product is zero, indicating no similarity.
- The inner product of two functions \(f(t)\) and \(g(t)\), defined on the interval \([a,b]\), is \[ \int_a^b f(t)g(t)\,dt, \] which can be approximated by \[ \int_a^b f(t)g(t)\,dt \approx \sum_{j=1}^n f(t_j)g(t_j) \Delta t, \] where \(\Delta t = \frac{b-a}{n}\) and \(t_j = a + j\Delta t\). Hence, \(\int_a^b f(t)g(t)\,dt\) can be viewed as the inner product of two vectors \( \mathbf{f} := (f(t_1), f(t_2), \ldots, f(t_n))\sqrt{\Delta t} \) and \(\mathbf{g} := (g(t_1), g(t_2), \ldots, g(t_n))\sqrt{\Delta t}: \) \[ \int_a^b f(t)g(t)\,dt \approx \mathbf{f} \cdot \mathbf{g}=\langle \mathbf{f}, \mathbf{g} \rangle. \]
The cross product of two vectors in three dimensions results in a vector perpendicular to both, defined as: \[ \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ u_x & u_y & u_z \\ v_x & v_y & v_z \end{vmatrix}. \]
- The magnitude is: \[ \|\mathbf{u} \times \mathbf{v}\| = \|\mathbf{u}\| \|\mathbf{v}\| \sin\theta, \] where \(\theta\) is the angle between the vectors.
- The vector cross product \(\mathbf{u} \times \mathbf{v}\) is perpendicular to both \(\mathbf{u}\) and \(\mathbf{v}\).
- The cross product is used to compute torque, which describes the rotational effect of a force: \[ \mathbf{\tau} = \mathbf{r} \times \mathbf{F}, \] where \(\mathbf{r}\) is the position vector from the axis of rotation to the point of force application. Click this link for a visual explanation.
The convolution product combines two functions and is widely used in signal processing applications.
- For a one-dimensional signal, the convolution of two functions \(f(t)\) and \(w(t)\) is defined as: \[ (f * w)(t) = \int_{-\infty}^\infty f(\tau) w(t - \tau) \, d\tau. \] In deep learning, convolution can be interpreted as an inner product between a kernel (filter) and a segment of the input signal. Click this link for a visual understanding of convolution.
- For discrete signals \(\mathbf{f} = [f_1, f_2, \ldots, f_N]\) and \(\mathbf{w} = [w_1, w_2, w_3]\), the convolution at position \(k\) can be written as: \[ (\mathbf{f} * \mathbf{w})_k = \langle \mathbf{w}, \mathbf{f}_{k:k+2} \rangle, \] where \(\mathbf{f}_{k:k+2}\) denotes the segment of \(\mathbf{f}\) starting at index \(k\) and spanning 3 elements.
- For image processing, convolution is similarly defined but extended to two dimensions. Let \(\mathbf{I}\) represent the 2D input image, and \(\mathbf{w}\) represent a \(3 \times 3\) kernel (filter). The convolution at position \((x, y)\) can be expressed as: \[ (\mathbf{I} * \mathbf{w})(x, y) = \langle \mathbf{w}, \mathbf{I}_{x:x+2, y:y+2} \rangle, \] where \(\mathbf{I}_{x:x+2, y:y+2}\) is the \(3 \times 3\) subregion of the image centered at position \((x, y)\), and the inner product is computed as: \[ \langle \mathbf{w}, \mathbf{I}_{x:x+2, y:y+2} \rangle = \sum_{i=1}^3 \sum_{j=1}^3 w(i, j) I(x+i-1, y+j-1). \] Convolution is thus a weighted sum, calculated via the inner product, where the weights are determined by the kernel \(\mathbf{w}\).
- This link shows how to compute the following convolution: \[ \underbrace{\begin{bmatrix} 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \end{bmatrix}}_{\mathbf{I}} * \underbrace{\begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}}_{\mathbf{w}} = \begin{bmatrix} 4 & 3 & 4 \\ 4 & 4 & 3 \\ 2 & 3 & 4 \end{bmatrix} \]
- This operation extracts features such as edges, textures, and patterns in images and is fundamental in deep learning for tasks like image recognition, object detection, and segmentation.
2. The Derivative: A Ratio in the Limiting Sense
The concept of a derivative is deeply connected to the idea of a ratio. Specifically, for a scalar function \(f(x)\) of a single variable \(x\), the derivative is the limit of the ratio of the change in the function's value (\(f(x)\), the dependent variable) to the change in its independent variable (\(x\), the independent variable). More precisely, the derivative is defined as: \[ f'(x) = \frac{d}{dx} f(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}. \] The derivative represents the instantaneous rate of change of \(f(x)\) with respect to \(x\), making it a ratio in the limiting sense. In practical terms, it quantifies the sensitivity of \(f(x)\) to small changes in \(x\), describing how the function's value changes locally.
- The product rule of derivatives states that the derivative of the product of two functions is given by: \[ \frac{d}{dx} [f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x) \cdot g'(x). \]
- Proof. The product rule for derivatives can be approximated using the difference quotient: \[ \frac{d}{dx} [f(x) \cdot g(x)] \approx \frac{f(x+\Delta x) g(x+\Delta x) - f(x) g(x)}{\Delta x}. \] This can be rewritten as: \[ \frac{d}{dx} [f(x) \cdot g(x)] \approx \underbrace{\frac{f(x+\Delta x) g(x+\Delta x) - f(x+\Delta x) g(x)}{\Delta x}}_{\textstyle f(x) g'(x)} + \underbrace{\frac{f(x+\Delta x) g(x) - f(x) g(x)}{\Delta x}}_{\textstyle f'(x) g(x)}. \]
- The chain rule of derivatives allows us to compute the derivative of a composite function. For a composite function \(y = f(g(x))\), \(\frac{dy}{dx}\) is written as: \[ \frac{d}{dx} f(g(x)) = f'(g(x)) \cdot g'(x). \]
- Proof. The chain rule for derivatives can also be approximated using the difference quotient: \[ \frac{d}{dx} f(g(x)) \approx \frac{f(g(x+\Delta x)) - f(g(x))}{\Delta x}. \] By introducing intermediate terms, this can be written as: \[ \frac{d}{dx} f(g(x)) \approx \underbrace{\frac{f(g(x+\Delta x)) - f(g(x))}{g(x+\Delta x) - g(x)}}_{\textstyle f'(g(x))} \cdot \underbrace{\frac{g(x+\Delta x) - g(x)}{\Delta x}}_{\textstyle g'(x)}. \] In the case where \(g(x)\) is locally constant, so \(g'(x) = 0\), the chain rule simplifies as \(\frac{d}{dx} f(g(x)) = f'(g(x)) \cdot 0 = 0. \)
- The linear approximation of a function \(f(x)\) near a point \(x = a\) uses the derivative to approximate the function as a straight line. The formula for the linear approximation is: \[ f(x) \approx f(a) + f'(a)(x - a), \] This formula gives the equation of the tangent line to \(f(x)\) at \(x = a\), which serves as the best linear approximation to \(f(x)\) near \(a\).
- Derivatives in Optimization. Derivatives are widely used in optimization problems to find the minimum or maximum value of a function. A critical point of a function occurs when the derivative is zero: \[ f'(x) = 0. \] To determine whether a critical point is a minimum or maximum, the second derivative \(f''(x)\) is evaluated:
- If \(f''(x) > 0\) (the function is convex), the critical point is a local minimum.
- If \(f''(x) < 0\) (the function is concave), the critical point is a local maximum.
- Newton’s Method for Finding Roots. Newton’s method is an iterative technique for solving equations of the form \(f(x) = 0\). The iterative formula is: \[x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)},\] where \(x_k\) is the current estimate, \(f(x_k)\) is the function value, and \(f'(x_k)\) is the derivative at \(x_k\). The idea of the update rule comes from the linear approximation: \[ f(x_{k+1}) \approx f(x_k) + f'(x_k)(x_{k+1} - x_k), \] with the hope that \(f(x_{k+1}) = 0\). Newton's method is widely used due to its fast convergence for well-behaved functions, particularly when the initial guess is close to the root. This link provides a visual understanding of Newton's method.
- Newton’s Method for Finding Minimum Points. Newton’s method can also be used to find minimum points of a function \(f(x)\), particularly in optimization problems. For this, the method solves:\[f'(x) = 0,\]using the following iterative formula:\[x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)},\]where \(f''(x_k)\) is the second derivative of the function. This approach ensures fast convergence to the critical point, provided that the initial guess \(x_0\) is close to the true minimum and the second derivative \(f''(x)\) is nonzero.
- Proof. The product rule for derivatives can be approximated using the difference quotient: \[ \frac{d}{dx} [f(x) \cdot g(x)] \approx \frac{f(x+\Delta x) g(x+\Delta x) - f(x) g(x)}{\Delta x}. \] This can be rewritten as: \[ \frac{d}{dx} [f(x) \cdot g(x)] \approx \underbrace{\frac{f(x+\Delta x) g(x+\Delta x) - f(x+\Delta x) g(x)}{\Delta x}}_{\textstyle f(x) g'(x)} + \underbrace{\frac{f(x+\Delta x) g(x) - f(x) g(x)}{\Delta x}}_{\textstyle f'(x) g(x)}. \]
- Proof. The chain rule for derivatives can also be approximated using the difference quotient: \[ \frac{d}{dx} f(g(x)) \approx \frac{f(g(x+\Delta x)) - f(g(x))}{\Delta x}. \] By introducing intermediate terms, this can be written as: \[ \frac{d}{dx} f(g(x)) \approx \underbrace{\frac{f(g(x+\Delta x)) - f(g(x))}{g(x+\Delta x) - g(x)}}_{\textstyle f'(g(x))} \cdot \underbrace{\frac{g(x+\Delta x) - g(x)}{\Delta x}}_{\textstyle g'(x)}. \] In the case where \(g(x)\) is locally constant, so \(g'(x) = 0\), the chain rule simplifies as \(\frac{d}{dx} f(g(x)) = f'(g(x)) \cdot 0 = 0. \)
- If \(f''(x) > 0\) (the function is convex), the critical point is a local minimum.
- If \(f''(x) < 0\) (the function is concave), the critical point is a local maximum.
3. Gradient
For a scalar function \(f(x, y, z)\) of multiple variables, the derivative with respect to a single variable is called a partial derivative. It is denoted as: \[ \frac{\partial f}{\partial x}, \quad \frac{\partial f}{\partial y}, \quad \frac{\partial f}{\partial z}. \] The partial derivative with respect to \(x\) is defined as: \[ \frac{\partial f}{\partial x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x, y, z) - f(x, y, z)}{\Delta x}, \] where \(y\) and \(z\) are held constant. Partial derivatives measure the rate of change of \(f(x, y, z)\) with respect to one variable, while treating the other variables as constants. They are fundamental in multivariable calculus and have applications in fields such as physics, engineering, and medical imaging.
The gradient of a scalar function \(f(x, y, z)\) is a vector that points in the direction of the steepest rate of increase of the function. It is defined as: \[ \nabla f = \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} + \frac{\partial f}{\partial z} \hat{k} = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right), \] where \(\frac{\partial f}{\partial x}\), \(\frac{\partial f}{\partial y}\), and \(\frac{\partial f}{\partial z}\) are the partial derivatives of \(f(x, y, z)\), and \(\hat{i}\), \(\hat{j}\), and \(\hat{k}\) are the unit vectors in the \(x\)-, \(y\)-, and \(z\)-directions, respectively. For a scalar function \(f(\mathbf{x})\) with \(\mathbf{x} = (x_1, x_2, \dots, x_n)\) in \(n\)-dimensional space, the gradient is given as: \[ \nabla f(\mathbf{x}) = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n} \right), \] where \(\frac{\partial f}{\partial x_i}\) represents the partial derivative of \(f(\mathbf{x})\) with respect to the \(i\)-th component of \(\mathbf{x}\). The gradient is a vector field that provides both the direction and magnitude of the steepest ascent of the function \(f\). The magnitude of the gradient, \(\|\nabla f\|\), quantifies the steepness of the increase and is calculated as: \[ \|\nabla f\| = \sqrt{\sum_{i=1}^n \left( \frac{\partial f}{\partial x_i} \right)^2}. \] The gradient is an essential tool in fields such as physics, optimization, and medical imaging, where it is used to analyze changes in scalar fields like temperature, pressure, or image intensity.
- Linear Regression with Gradient Descent. Let \(\boldsymbol{\Theta} = (\theta_0, \theta_1) \in \mathbb{R}^2\), and define the linear function: \[ f(x; \boldsymbol{\Theta}) = \theta_1 x + \theta_0 \in \mathbb{R}. \] The goal of linear regression is to find the parameters \(\boldsymbol{\Theta} = (\theta_0, \theta_1)\) that minimize the loss function: \[ \mathcal{L}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N \left( \theta_1 x_k + \theta_0 - y_k \right)^2, \] where \(x_k\) and \(y_k\) are the input and target values, respectively, and \(N\) is the total number of samples. The final objective is: \[ \boldsymbol{\Theta} = \underset{\boldsymbol{\Theta}}{\arg\min} \, \mathcal{L}(\boldsymbol{\Theta}). \] Here, the term "argmin" stands for "argument of the minimum", which returns the value of \(\boldsymbol{\Theta}\) that minimizes \(\mathcal{L}(\boldsymbol{\Theta})\).
- Gradient of the loss function. To minimize the loss function, we compute the gradient \(\nabla \mathcal{L}(\boldsymbol{\Theta})\): \[ \nabla_{\boldsymbol{\Theta}} \mathcal{L} (\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N 2\left( \theta_1 x_k + \theta_0 - y_k \right) \begin{bmatrix} 1 \\ x_k \end{bmatrix}. \]
- Gradient descent update rule. Using gradient descent, the parameters are updated iteratively as: \[ \boldsymbol{\Theta}^{(n+1)} = \boldsymbol{\Theta}^{(n)} - \alpha \nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta}^{(n)}), \] where:
- \(\boldsymbol{\Theta}^{(n)}\) represents the parameters at the \(n\)-th iteration,
- \(\alpha\) is the learning rate (a small positive scalar),
- \(\nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta})\) is the gradient of the loss function with respect to the parameters.
- Polynomial Regression with Gradient Descent. Let \(\boldsymbol{\Theta} = (\theta_0, \theta_1, \dots, \theta_L) \in \mathbb{R}^{L+1}\) be the parameters of the model. The polynomial regression function of degree \(L\) is defined as: \[ f(x; \boldsymbol{\Theta}) = \theta_L x^L + \dots + \theta_1 x + \theta_0. \]
- The goal of polynomial regression is to find the parameters \(\boldsymbol{\Theta}\) that minimize the mean squared loss function: \[ \mathcal{L}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right)^2, \] where:
- \(N\) is the number of data points,
- \(x_k\) and \(y_k\) represent the input and target values for the \(k\)-th data point.
- Gradient of the loss function. To minimize the loss function using gradient descent, we compute the gradient \(\nabla \mathcal{L}(\boldsymbol{\Theta})\) with respect to \(\boldsymbol{\Theta}\): \[ \nabla \mathcal{L}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N 2 \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \begin{bmatrix} 1 \\ x_k \\ \vdots \\ x_k^L \end{bmatrix}. \]
- Gradient descent update rule. The parameters are updated iteratively using the gradient descent rule: \[ \boldsymbol{\Theta}^{(n+1)} = \boldsymbol{\Theta}^{(n)} - \alpha \nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta}), \] where:
- \(\boldsymbol{\Theta}^{(n)}\) is the parameter vector at iteration \(n\), \item \(\alpha\) is the learning rate (a small positive scalar),
- \(\nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta})\) is the gradient of the loss function.
- Optimization objective. The optimization objective is to solve: \[ \boldsymbol{\Theta} = \underset{\boldsymbol{\Theta}}{\arg\min} \, \mathcal{L}(\boldsymbol{\Theta}). \]
- Overfitting. Although higher-degree polynomials can fit the training data very well, they are prone to overfitting. Overfitting occurs when the model captures noise in the training data, leading to poor generalization on unseen test data.
- Gradient Descent for a Two-Layer Neural Network. We are given the parameters \(\boldsymbol{\Theta} = (\theta_{10}, \theta_{11}, \theta_{20}, \theta_{21}) \in \mathbb{R}^4\) and the two-layer function: \[ f_1(x) = \sigma(\theta_{11} x + \theta_{10}), \quad f(x; \boldsymbol{\Theta}) = f_2 \circ f_1(x) = \sigma(\theta_{21} f_1(x) + \theta_{20}), \] where \(\sigma(\cdot)\) is the activation function. Here, we use the ReLU activation function \(\sigma(z)\) that is defined as: \[ \sigma(z) = \max(0, z), \] and its derivative \(\sigma'(z)\) is: \[ \sigma'(z) = \begin{cases} 1, & \text{if } z > 0, \\ 0, & \text{if } z \leq 0. \end{cases} \] The loss function to minimize is the mean squared error: \[ \mathcal{L}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right)^2, \] where \(\{ (x_k, y_k) : k = 1, \dots, N \}\) represents the training data.
- Gradient descent update rule. To minimize \(\mathcal{L}(\boldsymbol{\Theta})\), we compute the gradients of the loss function with respect to each parameter in \(\boldsymbol{\Theta}\): \[ \boldsymbol{\Theta}^{(n+1)} = \boldsymbol{\Theta}^{(n)} - \alpha \nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta}), \] where \(\alpha > 0\) is the learning rate.
- Gradient of the loss Function using the chain rule. The partial derivatives of \(\mathcal{L}(\boldsymbol{\Theta})\) with respect to the parameters are as follows:
- Partial derivative with respect to \(\theta_{21}\): \[ \frac{\partial \mathcal{L}}{\partial \theta_{21}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}) f_1(x_k). \]
- Partial derivative with respect to \(\theta_{20}\): \[ \frac{\partial \mathcal{L}}{\partial \theta_{20}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}). \]
- Partial derivative with respect to \(\theta_{11}\) (first layer weight): \[ \frac{\partial \mathcal{L}}{\partial \theta_{11}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}) \theta_{21} \sigma'(\theta_{11} x_k + \theta_{10}) x_k. \]
- Partial derivative with respect to \(\theta_{10}\) (first layer bias): \[ \frac{\partial \mathcal{L}}{\partial \theta_{10}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}) \theta_{21} \sigma'(\theta_{11} x_k + \theta_{10}). \]
- Gradient descent iterative updates. The parameters \(\boldsymbol{\Theta} = (\theta_{10}, \theta_{11}, \theta_{20}, \theta_{21})\) are updated iteratively as: \[ \theta_{ij}^{(n+1)} = \theta_{ij}^{(n)} - \alpha \frac{\partial \mathcal{L}}{\partial \theta_{ij}}, \] where \(\theta_{ij}\) represents any parameter in the vector \(\boldsymbol{\Theta}\).
- Importance of gradients in neural network learning. Gradients play a central role in neural network learning by guiding the optimization process. The gradient of the loss function with respect to each parameter provides information about the direction and rate of change of the loss. Specifically:
- Gradients indicate how to adjust the parameters to reduce the loss. A negative gradient points in the direction of decreasing loss.
- By iteratively updating parameters using the gradient descent rule, the neural network learns to approximate the target function or minimize prediction errors.
- The chain rule allows gradients to propagate backward through layers, enabling the adjustment of weights in multi-layer networks (backpropagation).
- Gradient of the loss function. To minimize the loss function, we compute the gradient \(\nabla \mathcal{L}(\boldsymbol{\Theta})\): \[ \nabla_{\boldsymbol{\Theta}} \mathcal{L} (\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N 2\left( \theta_1 x_k + \theta_0 - y_k \right) \begin{bmatrix} 1 \\ x_k \end{bmatrix}. \]
- Gradient descent update rule. Using gradient descent, the parameters are updated iteratively as: \[ \boldsymbol{\Theta}^{(n+1)} = \boldsymbol{\Theta}^{(n)} - \alpha \nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta}^{(n)}), \] where:
- \(\boldsymbol{\Theta}^{(n)}\) represents the parameters at the \(n\)-th iteration,
- \(\alpha\) is the learning rate (a small positive scalar),
- \(\nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta})\) is the gradient of the loss function with respect to the parameters.
- The goal of polynomial regression is to find the parameters \(\boldsymbol{\Theta}\) that minimize the mean squared loss function: \[ \mathcal{L}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right)^2, \] where:
- \(N\) is the number of data points,
- \(x_k\) and \(y_k\) represent the input and target values for the \(k\)-th data point.
- Gradient of the loss function. To minimize the loss function using gradient descent, we compute the gradient \(\nabla \mathcal{L}(\boldsymbol{\Theta})\) with respect to \(\boldsymbol{\Theta}\): \[ \nabla \mathcal{L}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{k=1}^N 2 \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \begin{bmatrix} 1 \\ x_k \\ \vdots \\ x_k^L \end{bmatrix}. \]
- Gradient descent update rule. The parameters are updated iteratively using the gradient descent rule: \[ \boldsymbol{\Theta}^{(n+1)} = \boldsymbol{\Theta}^{(n)} - \alpha \nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta}), \] where:
- \(\boldsymbol{\Theta}^{(n)}\) is the parameter vector at iteration \(n\), \item \(\alpha\) is the learning rate (a small positive scalar),
- \(\nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta})\) is the gradient of the loss function.
- Optimization objective. The optimization objective is to solve: \[ \boldsymbol{\Theta} = \underset{\boldsymbol{\Theta}}{\arg\min} \, \mathcal{L}(\boldsymbol{\Theta}). \]
- Overfitting. Although higher-degree polynomials can fit the training data very well, they are prone to overfitting. Overfitting occurs when the model captures noise in the training data, leading to poor generalization on unseen test data.
- Gradient descent update rule. To minimize \(\mathcal{L}(\boldsymbol{\Theta})\), we compute the gradients of the loss function with respect to each parameter in \(\boldsymbol{\Theta}\): \[ \boldsymbol{\Theta}^{(n+1)} = \boldsymbol{\Theta}^{(n)} - \alpha \nabla_{\boldsymbol{\Theta}} \mathcal{L}(\boldsymbol{\Theta}), \] where \(\alpha > 0\) is the learning rate.
- Gradient of the loss Function using the chain rule. The partial derivatives of \(\mathcal{L}(\boldsymbol{\Theta})\) with respect to the parameters are as follows:
- Partial derivative with respect to \(\theta_{21}\): \[ \frac{\partial \mathcal{L}}{\partial \theta_{21}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}) f_1(x_k). \]
- Partial derivative with respect to \(\theta_{20}\): \[ \frac{\partial \mathcal{L}}{\partial \theta_{20}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}). \]
- Partial derivative with respect to \(\theta_{11}\) (first layer weight): \[ \frac{\partial \mathcal{L}}{\partial \theta_{11}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}) \theta_{21} \sigma'(\theta_{11} x_k + \theta_{10}) x_k. \]
- Partial derivative with respect to \(\theta_{10}\) (first layer bias): \[ \frac{\partial \mathcal{L}}{\partial \theta_{10}} = \frac{2}{N} \sum_{k=1}^N \left( f(x_k; \boldsymbol{\Theta}) - y_k \right) \sigma'(\theta_{21} f_1(x_k) + \theta_{20}) \theta_{21} \sigma'(\theta_{11} x_k + \theta_{10}). \]
- Gradient descent iterative updates. The parameters \(\boldsymbol{\Theta} = (\theta_{10}, \theta_{11}, \theta_{20}, \theta_{21})\) are updated iteratively as: \[ \theta_{ij}^{(n+1)} = \theta_{ij}^{(n)} - \alpha \frac{\partial \mathcal{L}}{\partial \theta_{ij}}, \] where \(\theta_{ij}\) represents any parameter in the vector \(\boldsymbol{\Theta}\).
- Importance of gradients in neural network learning. Gradients play a central role in neural network learning by guiding the optimization process. The gradient of the loss function with respect to each parameter provides information about the direction and rate of change of the loss. Specifically:
- Gradients indicate how to adjust the parameters to reduce the loss. A negative gradient points in the direction of decreasing loss.
- By iteratively updating parameters using the gradient descent rule, the neural network learns to approximate the target function or minimize prediction errors.
- The chain rule allows gradients to propagate backward through layers, enabling the adjustment of weights in multi-layer networks (backpropagation).
4. Vector Fields
A vector field assigns a vector to every point in space. Examples include hemodynamics, where vector fields are used to understand blood flow patterns and detect abnormalities such as stenosis or aneurysms, and respiratory dynamics, where vector fields model airflow in the lungs to study ventilation efficiency.
Let \(\mathbf{r} = (x, y, z)\). A vector field is defined as: $$F(\mathbf{r}) = F_x(\mathbf{r}) \hat{i} + F_y(\mathbf{r}) \hat{j} + F_z(\mathbf{r}) \hat{k},$$ where:
- \( F_x(\mathbf{r}) \): The \(x\)-component of the vector field.
- \( F_y(\mathbf{r}) \): The \(y\)-component of the vector field.
- \( F_z(\mathbf{r}) \): The \(z\)-component of the vector field.
- \( \hat{i}, \hat{j}, \hat{k} \): Unit vectors in the \(x\)-, \(y\)-, and \(z\)-directions, respectively.
Vector fields also play a central role in computer vision. Motion between consecutive images is often represented by a vector field known as \emph{optical flow}. For each pixel location \( (x,y) \), a displacement vector \(\mathbf{v}(x,y) = (u(x,y), v(x,y))\) describes the local motion. Such vector fields are used in action recognition, video prediction, autonomous driving, and medical image registration. Motion is inherently directional and spatially continuous, making vector fields a natural mathematical representation. Smoothness and physical constraints can be imposed using tools from vector calculus.
Line Integral Along a Vector Field
The line integral of a vector field \(\mathbf{F}(\mathbf{r})\) along a curve \(C\) measures the work done by the field along the path. It is given by: \[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_C (F_x \, dx + F_y \, dy + F_z \, dz), \] where:
- \(C\) is the curve along which the integral is evaluated.
- \(\mathbf{F}(\mathbf{r}) = F_x \hat{i} + F_y \hat{j} + F_z \hat{k}\) is the vector field.
- \(d\mathbf{r} = dx \, \hat{i} + dy \, \hat{j} + dz \, \hat{k}\) is the differential element of the curve. \end{itemize}
- To reduce this line integral to a 1D integral, parameterize the curve \(C\) by a parameter \(t\), such that: \[ \mathbf{r}(t) = (x(t), y(t), z(t)), \quad t \in [a, b]. \] The differentials \(dx\), \(dy\), and \(dz\) are expressed as: \[ dx = \frac{dx}{dt} \, dt, \quad dy = \frac{dy}{dt} \, dt, \quad dz = \frac{dz}{dt} \, dt. \] Substituting these into the line integral, we have: \[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_a^b \left[ F_x(x(t), y(t), z(t)) \frac{dx}{dt} + F_y(x(t), y(t), z(t)) \frac{dy}{dt} + F_z(x(t), y(t), z(t)) \frac{dz}{dt} \right] dt. \]
- Example: Work Done Along a Helix. Let \(\mathbf{F}(\mathbf{r}) = z \, \hat{i} + x \, \hat{j} + y \, \hat{k}\), and consider the helix parameterized by: \[ \mathbf{r}(t) = (\cos t, \sin t, t), \quad t \in [0, 2\pi]. \] Then: \[ \frac{dx}{dt} = -\sin t, \quad \frac{dy}{dt} = \cos t, \quad \frac{dz}{dt} = 1. \] Substituting these into the line integral: \[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^{2\pi} \left[ z(-\sin t) + x(\cos t) + y(1) \right] dt, \] where \(x = \cos t\), \(y = \sin t\), and \(z = t\). Simplifying: \[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^{2\pi} \left[ t(-\sin t) + \cos t (\cos t) + \sin t (1) \right] dt. \] Further simplifications yield the final 1D integral: \[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^{2\pi} \left( -t\sin t + \cos^2 t + \sin t \right) dt. \]
- Example: Blood Flow Work Along an Artery. The line integral can quantify the work done by blood pressure as blood moves along a curved artery. Suppose the pressure field \(\mathbf{F}(x, y) = -y \hat{i} + x \hat{j}\) acts along a path \(C\), parameterized as \(\mathbf{r}(t) = t \hat{i} + t^2 \hat{j}\), \(0 \leq t \leq 1\). The line integral is: \[\int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^1 \mathbf{F}(\mathbf{r}(t)) \cdot \frac{d\mathbf{r}}{dt} \, dt.\] Substitute:\[\mathbf{F}(\mathbf{r}(t)) = -t^2 \hat{i} + t \hat{j}, \quad \frac{d\mathbf{r}}{dt} = \hat{i} + 2t \hat{j}.\] The dot product is:\[\mathbf{F} \cdot \frac{d\mathbf{r}}{dt} = (-t^2)(1) + (t)(2t) = -t^2 + 2t^2 = t^2.\]The integral becomes:\[\int_0^1 t^2 \, dt = \left[ \frac{t^3}{3} \right]_0^1 = \frac{1}{3}.\]The work done by the pressure field along the artery is \( \frac{1}{3} \, \text{units} \).
In artificial intelligence, training dynamics in continuous time are often modeled by the gradient flow equation \[\dot{\theta}(t) = - \nabla L(\theta(t)),\] where \( \theta(t) \in \mathbb{R}^n \) denotes the model parameters and \( L(\theta) \) is the loss function. The cumulative change in the loss along a training trajectory \( \theta(t) \) can be expressed as a line integral of the gradient field along the path in parameter space:\[\int_{\theta(t)} \nabla L \cdot d\theta.\]
Divergence Theorem
The Divergence Theorem relates the flux of a vector field through a closed surface to the divergence of the field within the enclosed volume. Mathematically:\[\iint_{\partial V} \mathbf{F} \cdot \mathbf{n} \, dS = \iiint_V (\nabla \cdot \mathbf{F}) \, dV,\] where:
- \( \mathbf{F} \): Vector field (e.g., flow velocity or electric field).
- \( \partial V \): Closed surface enclosing the volume \(V\).
- The divergence of a vector field \(\mathbf{F} \), denoted as \(\nabla \cdot \mathbf{F}\), is a scalar quantity that measures the rate at which the vector field spreads out or converges at a point. It is defined as: \[ \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}, \]
- Proof of Divergence Theorem
- Step 1: Verification for a Cuboid. Consider a cuboidal volume: \[ V = \{ (x, y, z) : 0 < x < a, 0 < y < b, 0 < z < c \}. \] The integral over \( V \) is: \[ \iiint_V \nabla \cdot \mathbf{F} \, dV = \iiint_V \left( \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} \right) dx \, dy \, dz. \] Using the Fundamental Theorem of Calculus for each dimension: - For \( F_x \), integrate over \( x \): \[ \int_0^a \frac{\partial F_x}{\partial x} \, dx = F_x(a, y, z) - F_x(0, y, z). \] - For \( F_y \), integrate over \( y \): \[ \int_0^b \frac{\partial F_y}{\partial y} \, dy = F_y(x, b, z) - F_y(x, 0, z). \] - For \( F_z \), integrate over \( z \): \[ \int_0^c \frac{\partial F_z}{\partial z} \, dz = F_z(x, y, c) - F_z(x, y, 0). \] Summing these contributions gives: \[ \iiint_V \nabla \cdot \mathbf{F} \, dV = \underbrace{\iint F_x(a, y, z) - F_x(0, y, z) \, dy \, dz}_{A_x} + A_y+A_z\] where \[ A_y +A_z=\iint F_y(x, b, z) - F_y(x, 0, z) \, dx \, dz + \iint F_z(x, y, c) - F_z(x, y, 0) \, dx \, dy. \] This matches the surface integral: \[ \iint_{\partial V} \mathbf{F} \cdot \mathbf{n} \, dS, \] validating the theorem for a cuboid.
- Step 2: Union of Two Cuboids. Let \( V_1 \) and \( V_2 \) be two cuboids, and let \( V = V_1 \cup V_2 \). The divergence theorem holds for each volume individually: \[ \iiint_{V_1} \nabla \cdot \mathbf{F} \, dV = \iint_{\partial V_1} \mathbf{F} \cdot \mathbf{n} \, dS, \quad \iiint_{V_2} \nabla \cdot \mathbf{F} \, dV = \iint_{\partial V_2} \mathbf{F} \cdot \mathbf{n} \, dS. \] At the common interface \( \partial V_1 \cap \partial V_2 \), the outward normal vectors \( \mathbf{n}_1 \) and \( \mathbf{n}_2 \) are opposite. Therefore, the flux through the common surface cancels: \[ \iint_{\partial V_1 \cap \partial V_2} \mathbf{F} \cdot \mathbf{n}_1 \, dS + \iint_{\partial V_2 \cap \partial V_1} \mathbf{F} \cdot \mathbf{n}_2 \, dS = 0. \] Thus, for the union \( V \): \[ \iiint_V \nabla \cdot \mathbf{F} \, dV = \iiint_{V_1} \nabla \cdot \mathbf{F} \, dV + \iiint_{V_2} \nabla \cdot \mathbf{F} \, dV = \iint_{\partial V} \mathbf{F} \cdot \mathbf{n} \, dS. \]
- Step 3: Generalization to Arbitrary Volumes: Any arbitrary volume \(V\) can be approximated as a union of cuboidal subvolumes.
Stokes' Theorem
Stokes' Theorem relates the circulation of a vector field, \(\oint_{\partial S} \mathbf{F} \cdot d\mathbf{r}\), around a closed curve to the surface integral of the curl of the field, \(\iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dA\), over a surface \(S\) bounded by that curve. That is,
\[\oint_{\partial S} \mathbf{F} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dA,\] where:
- \( \mathbf{F} \): Vector field (e.g., velocity field of blood flow).
- \(\nabla \times \mathbf{F}\): Curl of the vector field, defined as: \[ \nabla \times \mathbf{F} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_x & F_y & F_z \end{vmatrix}, \]
- \( \partial S \): Boundary curve of the surface \(S\).
- \( \mathbf{n} \): Unit normal vector to the surface \(S\).
- Proof.
- Step 1: Proof for the Special Case of a Rectangular Surface. Let \( S = \{ (x, y) : 0 < x < a, 0 < y < b \} \), a rectangular surface in the \( xy \)-plane. For this surface, the left-hand side of Stokes' Theorem becomes: \[ \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dx \, dy = \iint_S \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) dx \, dy. \] By integrating: \[ \int_0^b \int_0^a \frac{\partial F_2}{\partial x} dx \, dy = \int_0^b \left[ F_2(a, y) - F_2(0, y) \right] dy, \] and \[ \int_0^a \int_0^b \frac{\partial F_1}{\partial y} dy \, dx = \int_0^a \left[ F_1(x, b) - F_1(x, 0) \right] dx. \] The surface integral simplifies to: \[ \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dx \, dy = \int_0^b \left[ F_2(a, y) - F_2(0, y) \right] dy - \int_0^a \left[ F_1(x, b) - F_1(x, 0) \right] dx. \] For the boundary line integral, consider \( \partial S \), the rectangular contour traversed counter-clockwise: \[ \oint_{\partial S} \mathbf{F} \cdot d\boldsymbol{\ell} = \int_{(0, 0) \to (a, 0)} \mathbf{F} \cdot d\boldsymbol{\ell} + \int_{(a, 0) \to (a, b)} \mathbf{F} \cdot d\boldsymbol{\ell} + \int_{(a, b) \to (0, b)} \mathbf{F} \cdot d\boldsymbol{\ell} + \int_{(0, b) \to (0, 0)} \mathbf{F} \cdot d\boldsymbol{\ell}. \] Summing these contributions verifies Stokes' Theorem for the rectangular surface. ---
- Step 2: Proof for the Union of Two Regions. Let \( S = S_1 \cup S_2 \), where \( S_1 \) and \( S_2 \) are two adjacent regions with a shared boundary. Using the additivity of the surface integral: \[ \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dS = \iint_{S_1} (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dS + \iint_{S_2} (\nabla \times \mathbf{F}) \cdot \mathbf{n} \, dS. \] For the boundary integral, the shared boundary is traversed in opposite directions for \( \partial S_1 \) and \( \partial S_2 \), so the contributions cancel: \[ \oint_{\partial S_1} \mathbf{F} \cdot d\boldsymbol{\ell} + \oint_{\partial S_2} \mathbf{F} \cdot d\boldsymbol{\ell} = \oint_{\partial S} \mathbf{F} \cdot d\boldsymbol{\ell}. \] Thus, the theorem holds for \( S = S_1 \cup S_2 \). --
- Step 3: Generalization to Arbitrary Surfaces. Any arbitrary surface \( S \) can be approximated as a union of small planar elements. By applying the above steps to each small element and summing, Stokes' Theorem is proven for arbitrary surfaces.
- Example 1. Electromagnetic Field Analysis. In electromagnetism, Stokes' Theorem is used to relate the electric field \(\mathbf{E}\) and the magnetic field \(\mathbf{B}\) in Maxwell's equations. For instance: \[ \oint_{\partial S} \mathbf{E} \cdot d\mathbf{r} = -\iint_S \frac{\partial \mathbf{B}}{\partial t} \cdot \mathbf{n} \, dA, \] which describes Faraday's Law of electromagnetic induction. This law is fundamental in designing transformers, electric motors, and generators.
- Example 2. Fluid Flow and Circulation. In fluid dynamics, Stokes' Theorem is used to calculate the circulation of a velocity field \(\mathbf{v}\) around a closed path: \[ \oint_{\partial S} \mathbf{v} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{v}) \cdot \mathbf{n} \, dA. \] This is particularly useful for: - Measuring vorticity in turbulent blood flow. - Understanding circulation patterns in cardiovascular systems, such as near aneurysms or heart valves.
- Example 3. Medical Imaging and MRI. Stokes' Theorem is indirectly applied in Magnetic Resonance Imaging (MRI) to understand the relationship between changing magnetic fields and induced electric currents. Specifically, it helps model the spatial relationship between the magnetic gradient fields and the induced signal.
- Example 4. Magnetic Resonance-Based Blood Flow Analysis. Stokes' Theorem helps in determining circulation in blood flow using magnetic resonance imaging (MRI). The theorem relates the circulation of blood flow velocity along a closed path to the curl (vorticity) of the blood flow over a surface. This is useful in detecting abnormal flow patterns in arteries and veins.
- Example 5. Analysis of Eddy Currents in Conductors. Stokes' Theorem is used to analyze eddy currents in electromagnetic systems, such as in MRI or other diagnostic devices, by relating the circulation of induced currents to the curl of the magnetic field.
5. Basis as an Approximation of Functions
In mathematics and data science, the concept of a basis plays a fundamental role in approximating complex functions. A basis is a set of functions (or vectors) that can be combined to represent other functions within a given space. This idea allows us to break down a complicated object into simpler building blocks, making analysis, computation, and learning more tractable.
Basis: From \(n\)-Dimensional Vectors to Functions.
In \(n\)-dimensional space, a vector can be represented as a combination of basis vectors. For example, a vector \(\mathbf{v}\) in \(n\)-dimensional space can be written as: \[ \mathbf{v} = c_1 \mathbf{e}_1 + c_2 \mathbf{e}_2 + \cdots + c_n \mathbf{e}_n, \] where \(\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\) are the basis vectors, and \(c_1, c_2, \ldots, c_n\) are the coordinates of the vector with respect to this basis. The basis vectors provide a "coordinate system" for the space, allowing us to describe any vector in terms of these building blocks.
- For example, in 3D space, the standard basis vectors are: \[ \mathbf{e}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \quad \mathbf{e}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \quad \mathbf{e}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}. \] A vector \(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}\) can then be expressed as: \[ \mathbf{v} = v_1 \mathbf{e}_1 + v_2 \mathbf{e}_2 + v_3 \mathbf{e}_3. \]
Extending the Idea to Functions Just like vectors in \(n\)-dimensional space can be expressed using basis vectors, functions can be expressed as combinations of **basis functions**. For example, consider a function \(f(x)\). It can be approximated as: \[ f(x) \approx c_1 \phi_1(x) + c_2 \phi_2(x) + \cdots + c_n \phi_n(x), \] where \(\phi_1(x), \phi_2(x), \ldots, \phi_n(x)\) are the basis functions, and \(c_1, c_2, \ldots, c_n\) are the coefficients (analogous to the coordinates of a vector).
Why Is this Useful? Using basis functions to approximate a function is extremely useful in data science and applications like biology and medicine. For example:
- Polynomial Approximation: Using basis functions like \(1, x, x^2, \ldots, x^n\) to fit data.
- Fourier Series: Using sine and cosine functions as a basis to analyze periodic data.
- Wavelets: Using localized basis functions to analyze signals or images.
- Principal component analysis (PCA): Finding a basis that captures the maximum variance in data for dimensionality reduction.
In contrast, modern AI models do not approximate functions by selecting a fixed basis and refining coefficients. Instead, they construct nonlinear, selectively supported basis functions through learned feature transformations, bias-shifted hyperplanes, and nonlinear activation functions such as ReLU or sigmoid. This leads to adaptive, piecewise-linear (or piecewise-smooth) representations in which the effective basis depends on both the input and the learned parameters. Such representations underpin the expressive power and scalability of contemporary neural networks.
It is important to note, however, that deep neural networks should be understood as local interpolators, rather than global approximators. This is because they approximate the target function reliably only in neighborhoods of the training data distribution, which typically occupies only a small, structured subset of the overall input domain. This limitation follows directly from the training paradigm: network parameters are optimized by minimizing a loss function defined on a finite set of samples, which imposes no explicit constraint on the learned function outside data-supported regions. As a result, generalization beyond the observed data depends strongly on the inductive biases introduced by the network architecture, regularization strategies, and the structure of the training data itself.

















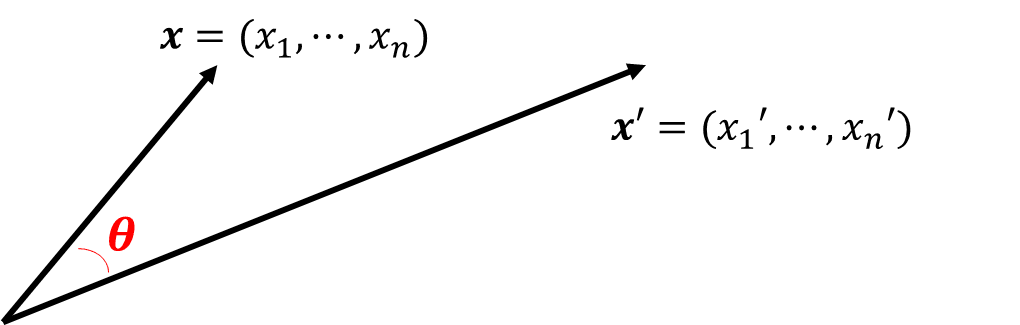
Comments
Post a Comment